안녕하세요!
리울(re_ul)입니다.

지난번 이론시간에 음이름과 계이름에 대해서 살펴봤습니다.
[음악통론] 음이름과 계이름: 음악의 기본을 이해하기
안녕하세요, 리울(Re_ul)입니다! 🎵 지난번에는 박자표에 대해서 공부해 봤습니다~ [음악통론] 박자표(Time Signature): 리듬을 결정하는 음악의 중심 기호안녕하세요,리울(Re_ul)입니다! 🎵 지난번
reul7.tistory.com
제 이론에 관한 글을 처음부터 보셨다면, 이제 악보를 보고 읽을 수 있는 단계가 되신 겁니다.
음악 이론을 통해서 곡을 바라보고, 곡을 분석, 작곡, 편곡 등등 을 하기 위한 첫 발을 떼신 것이라고 생각하면 좋을 거 같습니다. 계속해서 이론에 대해서 제가 공부한 내용들을 올려가겠습니다. 함께 파이팅 해봅시다!

이번 시간부턴 음악보단 수학에 가까운 "음정(Intervel)"에 대해서 알아보도록 하겠습니다!
처음 이 개념을 접하시는 분들에겐, 쉽지 않겠지만 이해만 하면 어렵지 않습니다!
한번 살펴볼까요?

음정(Intervel)이란?
음정은 두 음 사이의 거리, 즉 높낮이 차이를 나타내는 단위라고 생각하시면 됩니다.
음악 관련된 드라마, 예능, 오디션 프로그램 같은 것을 보면 가끔 "여기서 3도 위로 화음을 쌓아봐"라는 식으로 말을 하는 모습을 보신 적이 있을 겁니다.
여기서 "3도"가 바로 음정을 말하는 것인데, 3도면 해당 음을 포함해서 3번째 위에 있는 음을 이야기합니다.

네 ㅎㅎ 이해가 안 되신다고요?
좀 더 자세하게 설명을 드리겠습니다!
음정을 표기하는 방법
음정은 숫자로 표기합니다. 7개의 음을 기본으로 사용하게 되는데, 이유는 서양 음악 체계가 다이아토닉 스케일(Diatonic Scale)에 기반을 두고 있기 때문입니다.
지금 다이아토닉 스케일을 설명하기엔 머리가 복잡해지실 수 있으니 더 간단하게 말씀드리면!
- 우리가 피타고라스의 정리로 알고 있는 수학자 피타고라스가 수학적으로 음정 체계를 만들었는데, 이는 자연적인 진동수 비율을 기반으로 했기 때문에, 귀에 가장 조화롭게 들리는 음정들로 구성되었습니다. 이를 자연 음계라고 합니다.
- 이후 중세 유럽의 음악 이론가들이 이를 발전시켜 다이아토닉 스케일(7음 체계: 도레미파솔라시도)을 만들게 되었습니다. 지금 저희가 하고 있는 음악의 거의 대부분은 이 체계를 쓰기 때문에 1~7로 표기합니다. 숫자로 표기하고 옆에 "도"라는 단위를 붙이게 됩니다.
- "8도"는 흔히 우리가 말하는 옥타브[Octave → 라틴어 Octa(8)에서 유례]라고 합니다. 같은 이름의 음이지만, 높이만 다를 뿐 음색은 동일하게 느껴집니다.
전 음정을 설명할 때 계단이라고 생각하면 편하다고 이야기합니다. 기준 음은 1도입니다. 여기서 "몇 계단 위에 있는 음정인가?"를 생각하는 겁니다.

위의 그림처럼 "도" 음정의 3도 위는 "미"가 되는 겁니다.
너무 쉽죠?? 하지만.... 이제 본격적으로 들어가 볼까요?
음정의 성질
앞서 음정을 숫자로 표기하는 방법과 1도부터 7도까지의 음정 체계를 배웠다면, 이제 음정의 성질에 대해 알아보겠습니다. 음정의 성질은 음정이 가지고 있는 느낌이나 특성을 나타내는 것으로, 음악의 분위기와 조화를 결정하는 중요한 요소입니다.
음정의 성질에는 어떤 것들이 있을까요?
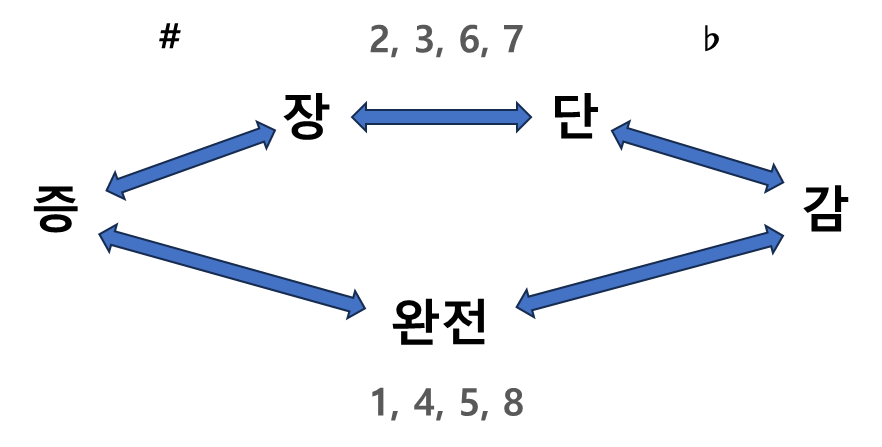
완전음정(Perfect, P)
- 1도, 4도, 5도, 8도는 자연스럽고 안정적인 소리를 만듭니다.
- 예: 도(C) → 솔(G) (완전 5도), 도(C) → 도(C) (완전 8도, 옥타브)
장음정(Major, M)
- 2도, 3도, 6도, 7도는 밝고 경쾌한 느낌을 줍니다.
- 예: 도(C) → 미(E) (장 3도), 도(C) → 라(A) (장 6도)
단음정(Minor, m)
- 장음정을 반음 낮춘 음정으로, 어둡고 감성적인 느낌을 줍니다.
- 예: 도(C) → 미♭(E♭) (단 3도), 도(C) → 라♭(A♭) (단 6도)
증음정(Augmented, Aug)
- 완전음정이나 장음정을 반음 높인 음정으로, 긴장감을 만듭니다.
- 예: 도(C) → 파#(F#) (증 4도)
감음정(Diminished, Dim)
- 완전음정이나 단음정을 반음 낮춘 음정으로, 불안정한 느낌을 줍니다.
- 예: 도(C) → 솔♭(G♭) (감 5도)
이해되시나요? 음정은 음과 음 사이의 간격이기 때문에, 기준이 되는음과 계산 하려고 하는 음정이 몇도고 그 간격이 멀어지는가 가까워 지는가? 이걸 확인 해야합니다.
예를 들어 볼까요??
- C 와 E 간격은 "장 3도(M3)" 입니다.
→ E♭을 하면 C와 E의 음정이 반음 가까워 졌죠? "단3도(m3)" 가 됩니다.
→ C♭을 하면 C와 E의 음정이 반음 멀어졌죠? "증3도(ang3)" 가 됩니다.
B 와 C♭은 이명동음(Enhamonic)입니다. B와 E는 4도 간격이지만, 기준이 C였기 때문에 증 3도 입니다.
결국 음정은 음과 음간의 간격, 거리 이기 때문에 기준이 되는 음정들의 위치에 따라서 달라지는 겁니다.
- D 와 F 간격은 "단 3도(m3)"입니다.
→ F#을 하면 D와 F의 간격이 반음 멀어졌죠? "장 3도(M3)" 입니다.
→ D♭을 하면 D가 반음을 내리면서 반음 멀어지게 됩니다. 이 역시도 "장 3도(M3)" 입니다.
왜 D와 F는 단 3도인지.... 이게 뭔말인지..... 많이 어렵죠?

당장은 어느정도 이해만 하시면 됩니다. 지금 이해를 하야 하는 건
- 음정은 "거리"를 나타낸다 입니다. 거리가 멀어지느냐? 가까워 지느냐?
- 기준 음과 계산하는 음은 어느정도의 간격을 가지고 있는가?
일단 이 정도만 기억하고 계시면 될거 같습니다. 조금 더 구체적인건 다음 시간에 장음계(Major Scale)와 함께 다루겠습니다.
'음악이론' 카테고리의 다른 글
| [음악기초이론] 스케일 디그리와 각 음의 역할, 자세히 알아보자 (0) | 2025.02.26 |
|---|---|
| [음악기초이론] 음계(Scale) : 음정의 수평적 이동 (0) | 2025.02.20 |
| [음악통론] 음이름과 계이름: 음악의 기본을 이해하기 (4) | 2024.12.27 |
| [음악통론] 박자표(Time Signature): 리듬을 결정하는 음악의 중심 기호 (2) | 2024.12.19 |
| [음악통론] 리듬을 그리는 기초: 음표 (1) | 2024.12.17 |